Аппроксимация функции
Задание. Построить таблицу значений функции F(x)=ax²+bx+c для 15 значений x в диапазоне –1 ≤ x ≤ +1, затем выполнить линейную и логарифмическую аппроксимацию функции и оценить ее погрешность. Построить графики этой функции и аппроксимирующих функций.
Как и в предыдущих задачах присваиваем имена ячейкам B2:B8, вводим исходные данные Xn, Xk, N, формулу для dX, коэффициенты a, b, c. Затем добавляем две небольшие таблички для коэффициентов линейной и логарифмической аппроксимации:
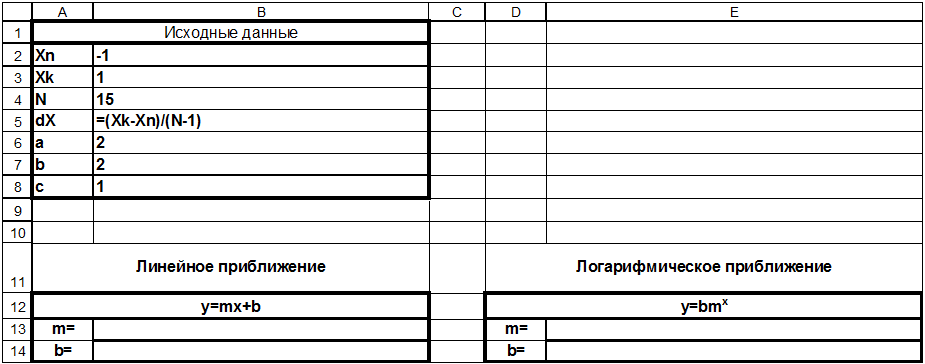
Ниже добавляем основную таблицу и заполняем столбцы x и F(x):
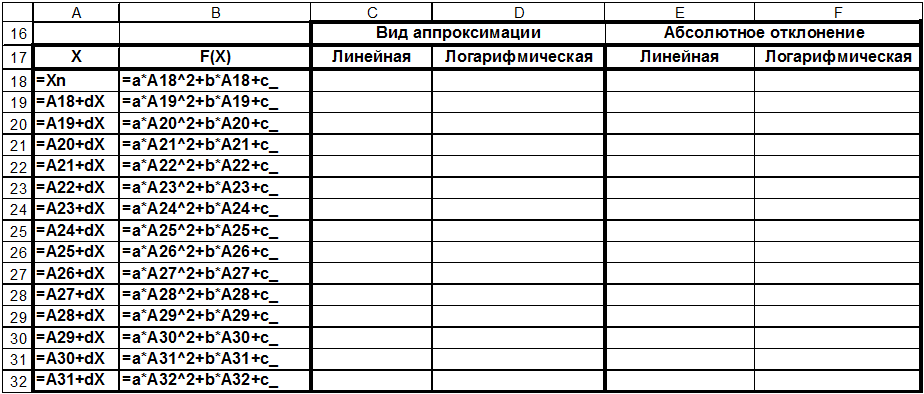
Теперь по известным значениям функции F(x) и аргумента функции x можно рассчитать коэффициенты соответствующих аппроксимирующих функций.
В ячейку B13 (коэффициент m для линейной интерполяции) запишем формулу =ИНДЕКС(ЛИНЕЙН(B18:B32;A18:A32);1).
В ячейку B14 (коэффициент b для линейной интерполяции) запишем формулу =ИНДЕКС(ЛИНЕЙН(B18:B32;A18:A32);2).
Функция ЛИНЕЙН - возвращает массив из двух элементов, являющихся коэффициентами прямой, которая наилучшим образом аппроксимирует имеющиеся данные для ряда с применением метода наименьших квадратов.
Функция ЛИНЕЙН имеет два обязательных параметра:
ЛИНЕЙН (известные значения Y; известные значения X)
В ячейке B13 функция ИНДЕКС выбирает значение первого элемента массива, возвращаемого функцией ЛИНЕЙН, в ячейке B14 функция ИНДЕКС выбирает значение второго элемента массива.
Для одномерного массива функция ИНДЕКС имеет два обязательных параметра:
ИНДЕКС(массив, номер элемента массива)
В ячейку E13 (коэффициент m для логарифмической интерполяции) запишем формулу =ИНДЕКС(ЛГРФПРИБЛ(B18:B32;A18:A32);1).
В ячейку E14 (коэффициент b для логарифмической интерполяции) запишем формулу =ИНДЕКС(ЛГРФПРИБЛ(B18:B32;A18:A32);2).
Функция ЛГРФПРИБЛ - возвращает массив из двух элементов, являющихся коэффициентами экспоненциальной кривой, которая наилучшим образом аппроксимирует имеющиеся данные для ряда с применением метода наименьших квадратов.
Функция ЛГРФПРИБЛ имеет два обязательных параметра:
ЛГРФПРИБЛ (известные значения Y; известные значения X)
В ячейке E13 функция ИНДЕКС выбирает значение первого элемента массива, возвращаемого функцией ЛГРФПРИБЛ, в ячейке E14 функция ИНДЕКС выбирает значение второго элемента массива.
В окончательном виде таблицы для коэффициентов будут выглядеть так:

Теперь, используя найденные коэффициенты, мы можем записать в ячейку C18 формулу для вычисления линейной функции =A18*$B$13+$B$14, а в ячейку D18 формулу для вычисления степенной функции =$E$14*СТЕПЕНЬ($E$13;A18) (=$E$14*$E$13^A18) и сделать автозаполнение столбцов C и D:
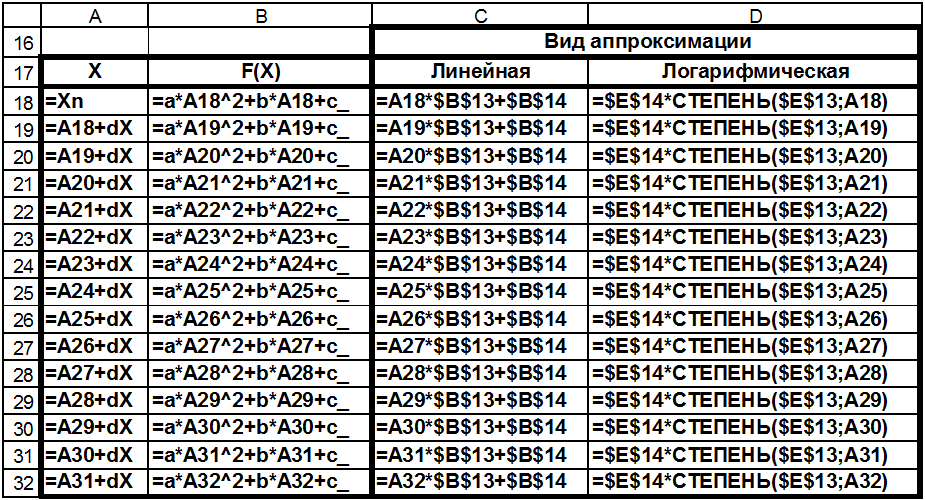
По четырем столбцам таблицы создаем диаграмму трех функций:
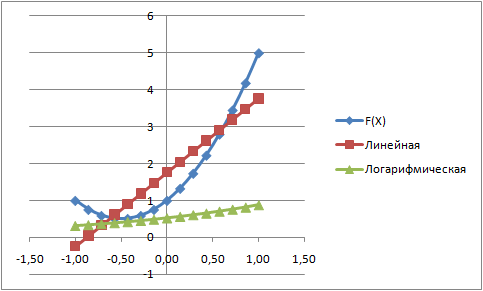
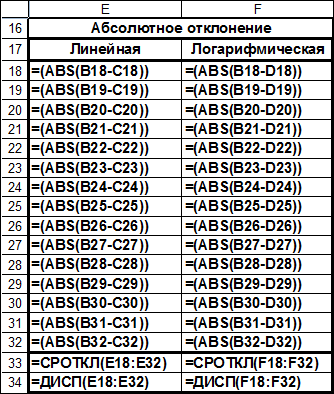
Теперь введем формулы абсолютного отклонения значений аппроксимирующих функций от соответствующих значений исходной функции. В ячейку E18 запишем формулу =(ABS(B18-C18)), а в ячейку F18 запишем формулу =(ABS(B18-D18)). Сделаем автозаполнение столбцов E и F.
Наконец запишем формулы для среднего отклонения и дисперсии отклонения. Для этого будем использовать статистические функции СРОТКЛ и ДИСП.
Правая часть основной таблицы примет окончательный вид: